순차 탐색(Sequential Search)
시작점부터 순차적으로 탐색하는 것
시간복잡도
10개의 데이터를 순차적으로 탐색했을 때 걸리는 평균 연산 횟수는

이고, 따라서 데이터의 크기가 n일 때 연산횟수는
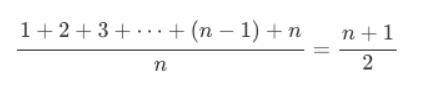
이므로 전부 탐색했을 때 시간복잡도는 O(n)이다.
사진 출처 : https://earthteacher.tistory.com/43#gsc.tab=0
구현
for (int i = 0; i < list.size(); i++) {
if(list.get(i) == searchItem)
return i;
}간단하게 살펴보면 리스트(또는 배열)가 있을 때, 첫 데이터부터 하나씩 가져와서 찾는 데이터와 비교한다.
가져온 데이터가 찾는 데이터와 일치하면 인덱스를 반환한다.
이진 탐색(Binary Search)
정렬된 데이터에서 중간 값을 찾는 값과 비교하여 탐색 범위를 줄여가며 탐색한다.
더 자세히 말하면, 길이가 n인 배열 arr[n]이 있을 때 arr[n/2] 값을 찾는 값과 비교한다. 찾는 값이 arr[n/2] 보다 작다면 0인덱스부터 n/2인덱스 사이의 중간 값을 찾아 또 비교하고, 찾는 값이 arr[n/2] 보다 크다면 n/2인덱스부터 마지막 인덱스의 중간 인덱스에 있는 값을 찾아 비교한다. 원하는 값을 찾을 때까지 이 과정을 반복한다.
시간복잡도
탐색하는 배열의 크기가 n일때 k번의 연산을 통해 값을 찾았다고 가정한다.
한번 연산을 할 때마다 탐색할 n의 수가 반으로 줄어든다 = *1/2
이때 k번이 지나면 원하는 값을 찾았으므로 k번 연산 후 탐색할 숫자는 1이 된다.
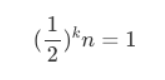
즉,

이므로 시간복잡도는

구현
반복문으로 구현
public static boolean BSearch(int[] arr, int n) {
int left = 0;
int right = arr.length - 1;
int mid;
while (left <= right) {
mid = (left + right) / 2;
if (arr[mid] < n) left = mid + 1;
else if (arr[mid] > n) right = mid - 1;
else return true;
}
return false;
}
재귀로 구현
public static boolean BSearchRecursive(int[] arr, int n, int left, int right) {
if(left > right) return false;
int mid = (left + right) / 2;
if (arr[mid] < n)
return BSearchRecursive(arr, n, mid +1, right);
else if (arr[mid] > n)
return BSearchRecursive(arr, n, left, mid - 1);
else
return true;
}
참고
- https://librewiki.net/wiki/%EC%8B%9C%EB%A6%AC%EC%A6%88:%EC%88%98%ED%95%99%EC%9D%B8%EB%93%AF_%EA%B3%BC%ED%95%99%EC%95%84%EB%8B%8C_%EA%B3%B5%ED%95%99%EA%B0%99%EC%9D%80_%EC%BB%B4%ED%93%A8%ED%84%B0%EA%B3%BC%ED%95%99/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98_%EA%B8%B0%EC%B4%88
- https://earthteacher.tistory.com/43#gsc.tab=0
- https://velog.io/@suk13574/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%9D%B4%EB%B6%84-%ED%83%90%EC%83%89-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-Binary-Search
